Eight Queens
How to play Eight Queens
Each game uses different controls, Games can a combination of mouse,keyboard and Joystick.
Eight Queens Description
The Eight Queens Problem
by John Sigle
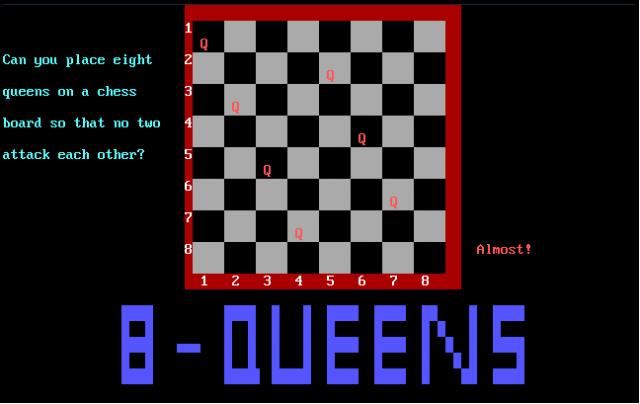
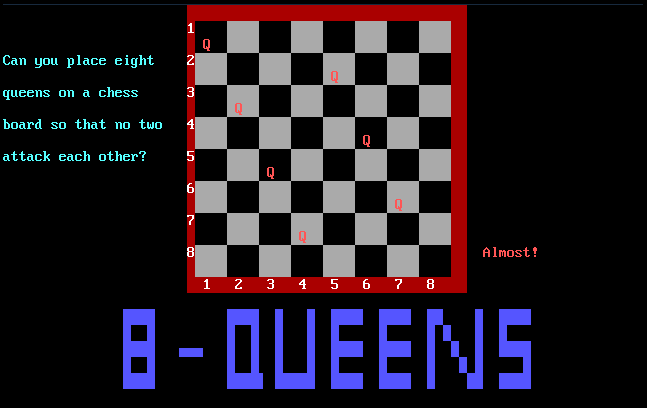
Can you place eight queens on a chess board so that no two are attacking each
other, that is, so that no two are on the same row, column, or diagonal? Yes,
it can be done! This program is an animated demonstration of an algorithm to
solve this problem. It is adapted from a program in the book ^1Algorithms + Data
^1Structures = Programs^0 by Niklaus Wirth, Prentice-Hall, 1976.
This program makes good use of recursion to search for a solution. It places
queens on the board column by column. In order to place eight queens safely on
the board, it places a queen safely in the first column and then tries to place
the seven remaining queens safely on the board. The latter problem (placing
seven queens safely) is the same problem as the original (placing eight queens)
only smaller in size. This leads to a recursive solution.
The program also illustrates backtracking, a method commonly used in
applications requiring searching, such as many areas of artificial intelligence.
When a "dead end" is reached (it is impossible to place any more of the
remaining queens safely) the most recently placed queen is removed from its
placement and advanced to a new position, if possible. If it cannot be advanced
then it is removed entirely and the next most recently placed queen is advanced,
and so on.
The choice of data structures in this program is also interesting. It does
not use a 2-dimensional array to represent the board as you might expect. The
most frequent task to be done by the program is testing to see if a position is
safe, that is, whether or not any queens lie on the same row or diagonal as that
position. The order of attempted queen placement (column by column) insures that
no queen lies on the same column. The data structures are chosen in order to
make the testing task convenient and efficient. "InRow" is a boolean array
whose i-th element indicates whether a queen has been placed in row i.
Similarly, "InDiag1" is a boolean array whose i-th element indicates whether a
queen has been placed in the i-th / diagonal (a / diagonal slants upward to the
right.) For the numbering scheme shown below, all the positions on a given /
diagonal have the same sum for their column and row numbers. This sum can be
used as an index to uniquely identify a / diagonal. These indices range from 2
thru 16. "InDiag2" records occupancy for the \ diagonals. The column number
minus the row number is constant for all positions on a \ diagonal, and is used
as an index, which ranges from -7 thru +7.
^C^I 1 * * * * * * * * ^N
^C^I 2 * * * * * * * * ^N
^C^I 3 * * * * * * * * ^N
^C^I 4 * * * * * * * * ^N
^C^I 5 * * * * * * * * ^N
^C^I 6 * * * * * * * * ^N
^C^I 7 * * * * * * * * ^N
^C^I 8 * * * * * * * * ^N
^C^I 1 2 3 4 5 6 7 8 ^N
This demo shows the PASCAL program as it executes as well as the data values
being manipulated. In addition it illustrates the program's actions on a chess
board. The demo can be run at varying speeds. It vividly shows the nature of
this searching method and relates it directly to the PASCAL program performing
the task.
You can control the speed by pressing a digit 0-9 (not the numeric keypad) at
any time. Nine is the highest speed while 1 is the lowest. A speed of 0 lets
you single-step through the program by pressing the spacebar twice to execute
each line of the program. Also, by pressing the + key you can switch between
two display modes: Full and Overview. In Full mode every line executed is
displayed. In Overview mode only selected lines, actually comment lines, are
displayed. In Overview mode the demo proceeds more quickly, yet shows the
highlights of the process. You can scroll the program display forward or
backward at any time by means of the up or down arrows. At the conclusion of
the demo the total number of positions tested and queen placements performed is
reported.